数Ⅲ 無限級数の基本&応用問題　解説付き　意外と忘れてるところがあるかも？

では早速やっていきましょう。

問題

(1)次の無限級数の収束、発散を調べ、収束するものはその和を求めよ。

①$\displaystyle \sum_{n=1}^{\infty}\frac{n}{n+1}$

②$\displaystyle \sum_{n=1}^{\infty}\frac{1}{2^n} \sin^2 \frac{nπ}{2}$

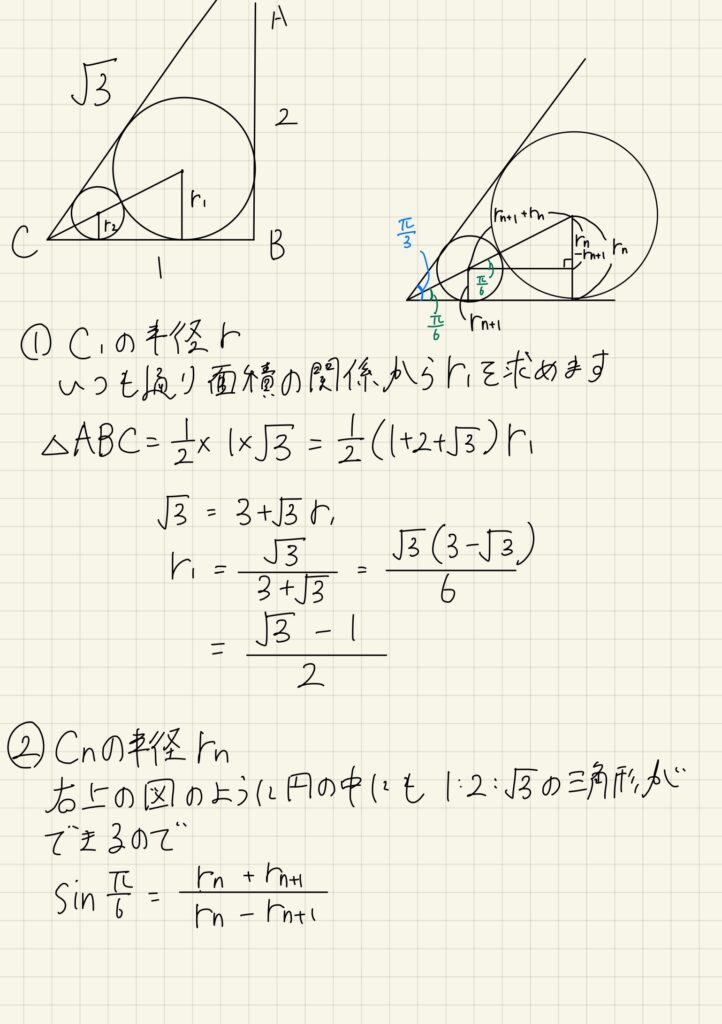
(2)直角三角形ABC(AB=2, BC=1, CA=$\sqrt{3}$)に内接する円を$C_1$とし、2辺AB, BCと円$C_1$に接する円を$C_2$, 2辺AB, BCと円$C_2$に接する円を$C_3$, 以下同様に$C_4 , C_5 , …C_n …$を作る。

①$C_1$の半径$r_1$を求めよ。

②$C_n$の半径$r_n$を求めよ。

③$C_n$の面積を$S_n$とするとき、$\displaystyle \sum_{n=1}^{\infty}S_n$を求めよ。

(3)

①x>0のとき$1<\sqrt{1+x}<1+x$が成り立つことを証明せよ。

②$\displaystyle \lim_{n \to \infty} \frac{1}{n}\displaystyle \sum_{k=1}^{n}\sqrt{1+\frac{k}{n^2}}$の値を求めよ。

解答

(1)

①

②

(2)

(3)

問題は以上です、お疲れ様でした。

まだ行けるよって方は下もどうぞ。

数II 三角関数の練習問題です。常に範囲に気をつけましょう。回答と解説、コラム付き